-
广度优先搜索
引言
在求解 leetcode 17 时,我遇到了BFS(广度优先搜索)这个概念。在深入了解后发现,BFS是图(graph)的一个知识点,我对这一知识点进行展开学习,并将找到的资料汇总起来。本文主要整理了图和广度优先搜索的相关知识点。
图的存储方式
研究图就需要使用计算机语言对其进行描述。图的存储结构除了要存储图中各个顶点的本身的信息外,同时还要存储顶点与顶点之间的所有关系(边的信息)。因此,图的结构比较复杂,很难以数据元素在存储区中的物理位置来表示元素之间的关系,但也正是由于其任意的特性,故物理表示方法很多。常用的图的存储结构有邻接矩阵、邻接表、十字链表和邻接多重表。
相邻矩阵(adjacency martix)
对于一个具有
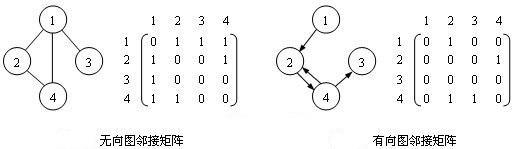
n个顶点的图,可以使用n*n的矩阵(二维数组)来表示它们间的邻接关系。下图中,矩阵A(i,j)=1表示图中存在一条边(Vi,Vj),而A(i,j)=0表示图中不存在边(Vi,Vj)。实际编程时,当图为不带权图时,可以在二维数组中存放bool值,A(i,j)=true表示存在边(Vi,Vj),A(i,j)=false表示不存在边(Vi,Vj);当图带权值时,则可以直接在二维数组中存放权值,A(i,j)=null表示不存在边(Vi,Vj)。
左图所示的是无向图的邻接矩阵表示法,可以观察到,矩阵延对角线对称,即
A(i,j)=A(j,i)。无向图邻接矩阵的第i行或第i列非零元素的个数其实就是第i个顶点的度。这表示无向图邻接矩阵存在一定的数据冗余。右图所示的是有向图邻接矩阵表示法,矩阵并不延对角线对称,
A(i,j)=1表示顶点Vi邻接到顶点Vj;A(j,i)=1则表示顶点Vi邻接自顶点Vj。两者并不象无向图邻接矩阵那样表示相同的意思。有向图邻接矩阵的第i行非零元素的个数其实就是第i个顶点的出度,而第i列非零元素的个数是第i个顶点的入度,即第i个顶点的度是第i行和第i列非零元素个数之和。由于存在
n个顶点的图需要n^2个数组元素进行存储,当图为稀疏图时,使用邻接矩阵存储方法将出现大量零元素,照成极大地空间浪费,这时应该使用邻接表表示法存储图中的数据。邻接表(adjacency list)
邻接表(adjacency list)是一种常用的表示图的数据结构。邻接表是许多链表的集合,每个链表描述了一个顶点(
vectex)的相邻元素(Neighbor)。更形象地讲,邻接表是一个二维容器,第一维描述某个点,第二维描述这个点所对应的边集们。
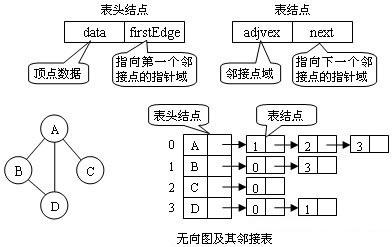
图的邻接矩阵存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。邻接表由表头结点和表结点两部分组成,其中图中每个顶点均对应一个存储在数组中的表头结点。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中。如下图所示,表结点存放的是邻接顶点在数组中的索引。对于无向图来说,使用邻接表进行存储也会出现数据冗余,表头结点A所指链表中存在一个指向C的表结点的同时,表头结点C所指链表也会存在一个指向A的表结点。
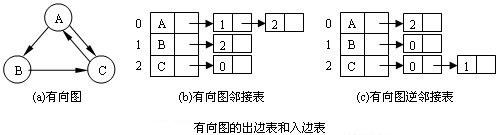
有向图的邻接表有出边表和入边表(又称逆邻接表)之分。出边表的表结点存放的是从表头结点出发的有向边所指的尾顶点;入边表的表结点存放的则是指向表头结点的某个头顶点。如下图所示,图(b)和(c)分别为有向图(a)的出边表和入边表。

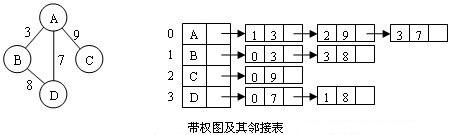
以上所讨论的邻接表所表示的都是不带权的图,如果要表示带权图,可以在表结点中增加一个存放权的字段,其效果如下图所示。

观察上图可以发现,当删除存储表头结点的数组中的某一元素,有可能使部分表头结点索引号的改变,从而导致大面积修改表结点的情况发生。可以在表结点中直接存放指向表头结点的指针以解决这个问题(在链表中存放类实例即是存放指针,但必须要保证表头结点是类而不是结构体)。在实际创建邻接表时,甚至可以使用链表代替数组存放表头结点或使用顺序表存代替链表存放表结点。本节所有的图片摘自 cnblogs.com - abatei
图的遍历
和树的遍历类似,在此,我们希望从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫做图的遍历(traversing graph)。如果只访问图的顶点而不关注边的信息,那么图的遍历十分简单,使用一个
foreach语句遍历存放顶点信息的数组即可。但如果为了实现特定算法,就需要根据边的信息按照一定顺序进行遍历。图的遍历算法是求解图的连通性问题、拓扑排序和求关键路径等算法的基础。图的遍历要比树的遍历复杂得多,由于图的任一顶点都可能和其余顶点相邻接,故在访问了某顶点之后,可能顺着某条边又访问到了已访问过的顶点,因此,在图的遍历过程中,必须记下每个访问过的顶点,以免同一个顶点被访问多次。为此给顶点附设访问标志
visited,其初值为false,一旦某个顶点被访问,则其visited标志置为true。图的遍历方法有两种:一种是深度优先搜索遍历(depth first search 简称DFS),另一种是广度优先搜索遍历(breadth first search 简称BFS)。
广度优先搜索(breadth first search)
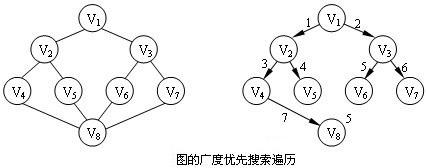
图的广度优先搜索遍历算法是一个分层遍历的过程,和二叉树的广度优先搜索遍历类同。它从图的某一顶点
Vi出发,访问此顶点后,依次访问Vi的各个未曾访问过的邻接点,然后分别从这些邻接点出发,直至图中所有已有已被访问的顶点的邻接点都被访问到。对于无向连通图,若顶点Vi为初始访问的顶点,则广度优先搜索遍历顺序如下所示。
广度优先搜索的伪代码如下:
BFS (G, s) // Where G is the graph and s is the source node let Q be queue. Q.enqueue( s ) // Inserting s in queue until all its neighbour vertices are marked. mark s as visited. while ( Q is not empty ) // Removing that vertex from queue, whose neighbour will be visited now v = Q.dequeue( ) // processing all the neighbours of v for all neighbours w of v in Graph G if w is not visited Q.enqueue( w ) // Stores w in Q to further visit its neighbour mark w as visited.时间复杂度
BFS的时间复杂度为O(V+E),其中V是节点的数量,E是边的数量。BFS的应用场景
- 最短路径问题
- P2P网络,网络广播
- GPS导航系统
- 搜索引擎的网络爬虫
- 最短路径问题
-
每周算法:拨号键盘上的字符组合
Description
Given a string containing digits from
2-9inclusive, return all possible letter combinations that the number could represent.A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
1 2abc 3def 4ghi 5jkl 6mno 7pqrs 8tuv 9wxyz Example:
Input: "23" Output: ["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
Note:
Although the above answer is in lexicographical order, your answer could be in any order you want.Solution
Approach 1
借助加法计算进位的思想,下面是我的解法。我首次提交时并没有注意输入字符串为空的情况,对于输入参数的检查还是太容易忽略了。
vector<string> letterCombinations(string digits) { vector<string> ans; if (digits.empty()) { return ans; } vector<string> letters {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}; vector<int> carry(nums.size(), 0); vector<int> nums; for (char ch : digits) { int n = ch - '0'; nums.push_back(n); } do{ string str; for (size_t i=0; i<carry.size(); ++i) { str += letters[nums[i]] [carry[i]]; } ans.push_back(str); int c = 1; for (int i=carry.size()-1; i >= 0; --i) { int d = carry[i] + c; if (d >= letters[nums[i]].size()) { carry[i] = 0; c = 1; } else { carry[i] = d; c = 0; break; } } if ( 1 == c) { break; } } while (1); return ans; }
我在想的是这个算法的时间复杂度是多少,感觉它的时间复杂度应该是O(n2)。
Approach 2 recursive
使用递归完成字符串的拼接,在每次递归,都会增加一个字符。终止递归的条件是字符串长度达到输入参数的长度。递归方法符合生活中的使用场景,还是比较容易理解的。
class Solution { char mMap[8][4] = { {'a', 'b', 'c', '#'}, {'d', 'e', 'f', '#'}, {'g', 'h', 'i', '#'}, {'j', 'k', 'l', '#'}, {'m', 'n', 'o', '#'}, {'p', 'q', 'r', 's'}, {'t', 'u', 'v', '#'}, {'w', 'x', 'y', 'z'}, }; public: vector<string> letterCombinations(string digits) { vector<string> result; backTrack(digits, result, "", 0); return result; } void backTrack(string &digits, vector<string> &result, string combination, int index) { if (index >= digits.length()) { if (combination.empty()) { return; } result.push_back(combination); return; } for (char c : mMap[digits[index] - '2']) { if (c == '#') continue; combination += c; backTrack(digits, result, combination, index+1); // 这里为什么要删去最后一个呢? // 因为之前在尾部追加了一个c combination.erase(combination.end() - 1); } } };
如何评估递归算法的时间复杂度和空间复杂度呢?Approach 3 BFS
宽度优先搜索,breadth-first search(BFS),是一种对树(tree)或图(graph)的遍历算法,下面就是这种算法的解法,代码使用java编写。
public List<String> letterCombinations(String digits) { LinkedList<String> ans = new LinkedList<String>(); if(digits.isEmpty()) { return ans; } String[] mapping = new String[] {"0", "1", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}; ans.add(""); for(int i=0; i<digits.length(); i++) { int x = Character.getNumericValue(digits.charAt(i)); while(ans.peek().length() == i) { String t = ans.remove(); // remove是从头部删去一个元素 for(char s : mapping[x].toCharArray()) { ans.add(t+s); // add是向尾部添加一个元素 } } } return ans; }
下面是另外一种使用BFS算法实现的解法
public List<String> letterCombinations(String digits) { LinkedList<String> ans = new LinkedList<String>(); if(digits.isEmpty()) { return ans; } String[] mapping = new String[] {"0", "1", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}; ans.add(""); while(ans.peek().length() != digits.length()){ String remove = ans.remove(); String map = mapping[digits.charAt(remove.length())-'0']; for(char c: map.toCharArray()){ ans.addLast(remove+c); } } return ans; }
Reference
-
每周算法:最接近的三数之和
Description
Given an array nums of n integers and an integer target, find three integers in nums such that the sum is closest to target. Return the sum of the three integers. You may assume that each input would have exactly one solution.
Example:
Given array nums = [-1, 2, 1, -4], and target = 1. The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).
Solution
Approach 1
这道题与之前的“3Sum”十分类似,做起来思路是非常相似的,最容易想到的就是暴力解法,穷举出所有的组合,进而找出最接近的。
int threeSumClosest(vector<int>& nums, int target) { if (nums.size() < 3) { return 0; } int ans = nums[0] + nums[1] + nums[2]; int diff = abs(target - ans); // 穷举出所有的组合,与target比较,找到最接近的 for (int i=0; i < nums.size(); ++i) { for (int j=i+1; j < nums.size(); ++j) { for (int k=j+1; k < nums.size(); ++k) { int sum_t = nums[i] + nums[j] + nums[k]; int diff_t = abs(target - sum_t); ans = diff_t < diff ? (diff = diff_t, sum_t) : ans; if (ans == target) { return ans; } } } } return ans; }
Approach 2
套用之前“3Sum”的O(n2)解法,下面的解法也是很容易想到的。
int threeSumClosest(vector<int>& nums, int target) { if (nums.size() < 3) { return 0; } sort(nums.begin(), nums.end()); int ans = nums[0] + nums[1] + nums[2]; int diff = abs(target - ans); for (int i=0; i < nums.size(); ++i) { int n1 = nums[i]; int front = i + 1; int end = nums.size() - 1; while (front < end) { int n2 = nums[front]; int n3 = nums[end]; int sum = n1 + n2 + n3; int diff_t = abs(target - sum); if (diff > diff_t) { ans = sum; diff = diff_t; } if (sum == target) { return sum; } else if (sum > target) { --end; } else { ++front; } } } return ans; }
Reference
-
在shell中使用正则表达式
引言
本篇文章主要是针对shell中的
grep和egrep的讲解,对于正则表达式的规则本身并没有太多的内容。在阅读本篇文章之前,读者应该对正则表达式有个大致的了解。grep命令grep命令是linux终端中最常用的命令之一,它的全称是“global regular expression print”,从字面上理解,grep可以用来进行正则表达式匹配。常用选项
使用一些选项命令能够更加方便地进行匹配-i忽略大小写-v进行逆向匹配-n打印行号--color=auto彩色输出结果支持的表达式
正则表达式有很多规则,grep支持的有如下:
在每一行的开始grep "^GUN" GPL-3
在每一行的结尾
grep "and$" GPL-3
匹配任意字符
grep "..cept" GPL-3
在指定的字符中进行匹配
grep "t[wo]o" GPL-3
在指定的字符中进行逆向匹配
grep "[^c]ode" GPL-3
使用范围来指定字符
grep "^[A-Z]" GPL-3
限定出现的次数为0次或0次以上
grep "([A-Za-z ]*)" GPL-3
egrep命令egrep的含义为“extended grep”,相对于grep有更多的正则表达式特性。同样,可以在使用grep时增加-E参数获得相同的效果。表达式分组
使用括号能够将表达式进行分组,下面的任何一个都能够实现这个效果grep "\(grouping\)" file.txt grep -E "(grouping)" file.txt egrep "(grouping)" file.txt
表达式进行中多选一
egrep "(GPL|General Public License)" GPL-3
匹配的重复次数为0次或0次以上,与
*限定符类似,但是?可以作用于一组字符egrep "(copy)?right" GPL-3
指定匹配的重复次数
egrep "[AEIOUaeiou]{3}" GPL-3
-
线程与进程的比较
进程与线程之间有什么区别
进程(process)是指在系统中正在运行的一个应用程序,是系统资源分配的基本单位,在内存中有其完备的数据空间和代码空间,拥有完整的虚拟空间地址。一个进程所拥有的数据和变量只属于它自己。
线程(thread)是进程内相对独立的可执行单元,所以也被称为轻量进程(lightweight processes)。线程是操作系统进行任务调度的基本单元,它与父进程的其它线程共享该进程所拥有的全部代码空间和全局变量,但拥有独立的堆栈(即局部变量对于线程来说是私有的)。
进程和线程都具有就绪、阻塞和运行三种基本状态。
联系
- 一个进程至少拥有一个线程(主线程),也可以拥有多个线程
- 一个线程必须有一个父进程,多个进程可以并发执行
- 一个线程可以创建和撤销另一个线程
- 同一个进程中的多个线程之间可以并发执行
区别
系统开销:在创建或撤消进程时,由于系统都要为之分配和回收资源,导致系统的开销明显大于创建或撤消线程时的开销
资源管理:进程有独立的地址空间,一个进程崩溃后,在保护模式下不会对其它进程产生影响,而线程只是一个进程中的不同执行路径。线程有自己的堆栈和局部变量,但线程之间没有单独的地址空间,一个线程死掉就等于整个进程死掉,所以多进程的程序要比多线程的程序健壮,但在进程切换时,耗费资源较大,效率要差一些。但对于一些要求同时进行并且又要共享某些变量的并发操作,只能用线程,不能用进程。通信方式
进程间通信主要包括管道、系统IPC(包括消息队列,信号量,共享存储)、SOCKET,具体说明参考linux进程间通信方式。进程间通信其实是指分属于不同进程的线程之间的通讯,所以进程间的通信方法同样适用于线程间的通信。但对于同一进程的不同线程来说,使用全局变量进行通信效率会更高。
什么情况下适合使用线程
线程相对于进程的优势:
- 线程间通信(数据交互)比进程间通信更加简便快捷。
- 线程之间的上下文切换速度要比进程间的快,也就是说,对于操作系统而言,停止一个线程并启动另一个线程的速度比进程之间相似操作更快。
- 创建一个线程的速度比创建一个进程的速度快。
下面的一些情景更适合使用线程来完成:
- 进行耗时较长的处理:当一个windows界面程序正在计算时,它就不能处理其他消息(message)了,界面就不能及时更新。
- 进行后台处理:有些任务并不是时间紧迫的,但是需要定期执行。
- 进行
I/O处理:I/O操作或网络操作一般都会有一定的延迟,线程能保证程序中的其他部分不会受到延迟的影响。
什么情况下适合使用进程
进程相对于线程的优势:
- 多线程系单进程的软件只能运行在一台机器上,而多进程的软件可以运行在多台机器上。这在一定程度上限制软件的可拓展性,单台机器的性能总是有限的。
- 多进程模型的鲁棒性更好,有更好的容错性。运行在同一进程下的多个线程会相互影响,如果其中的一个线程出了问题,可能会波及整个进程。
- 有些功能模块并不是线程安全的,这时就只能使用多进程模型了。
以chrome浏览器为例,它使用了多进程模型。每一个标签页都是一个进程,这样能够将渲染引擎中的bug隔离在该进程内,从而使整个程序免受影响。多进程模型将JavaScript隔离在每个进程中,这样就能防止其因占用过多的CPU或内存,使整个软件失去响应。另一方面,多进程模型的系统开销也是比较大的,这点能够从chrome的高额内存使用中看出来。不过chrome的优化策略可以让较低内存的情况下有更好内存使用效率。当一个标签页处于非激活状态,其对应的内存可以在需要时被交换进硬盘中,这样用户当前操作的页面就能够保持响应状态。如果使用的是多线程模型,区分活跃内存和非活跃内存就变得十分困难,导致内存使用效率的下降。
- 一个进程至少拥有一个线程(主线程),也可以拥有多个线程
-
每周算法:三数之和
Description
Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.
Note:
The solution set must not contain duplicate triplets.Example:
Given array nums = [-1, 0, 1, 2, -1, -4], A solution set is: [ [-1, 0, 1], [-1, -1, 2] ]
Solution
Approach 1
这道题有点难度,第一时间没有什么思路。我想到的主要问题是如何保证返回结果中不包含重复的一组数。如果使用暴力解法,将所有满足条件的组合取到后进行重复性清洗,应该是一种可行的解法,只是这样做时间复杂度有点高。
下面的代码就是暴力解法的实现。不出意外,在leetcode中结果为超时。这种算法的时间复杂度为
O(n^3 * nlogn) + O(n^2)。vector<vector<int>> threeSum(vector<int>& nums) { vector<vector<int>> ans; for (size_t i=0; i<nums.size(); ++i) { int n1 = nums[i]; for (size_t j=i+1; j<nums.size(); ++j) { int n2 = nums[j]; for (size_t k=j+1; k<nums.size(); ++k) { int n3 = nums[k]; if (n1 + n2 + n3 == 0) { vector<int> triplet{n1, n2, n3}; sort(triplet.begin(), triplet.end()); ans.push_back(triplet); } } } } // 将结果中的重复组合删掉 for (vector<vector<int>>::iterator it1 = ans.begin(); it1 != ans.end(); ++it1) { for (vector<vector<int>>::iterator it2=it1+1; it2!=ans.end();) { if (*it1 == *it2) { it2 = ans.erase(it2); } else { ++it2; } } } return ans; }
从上面这个解法中,我能够得到的
教训经验是对vector进行具有删除操作的循环时,使用迭代器完成更不容易出错。我之前的去重逻辑是这样的。for (int i=0; i<ans.size(); ++i) { for (int j=i+1; j<ans.size(); ++j) { if (ans[i] == ans[j]) { ans.erase(ans.begin() + j); } } }
很显然,上面的代码在一些情况下并不能彻底删去所有重复的元素,下面的代码才是真正正确的实现。
for (int i=0; i<ans.size(); ++i) { for (int j=i+1; j<ans.size();) { if (ans[i] == ans[j]) { ans.erase(ans.begin() + j); } else { ++j; } } }
Approach 2
我认为这到题的主要难点啊主要是在去除重复的问题上。下面的解法来自 leetcode ,在处理重复性问题时,在匹配答案时将重复的数字跳过,这样就不用在后续的结果中进行剔除重复元素的步骤了。
vector<vector<int> > threeSum(vector<int> &num) { std::sort(num.begin(), num.end()); vector<vector<int> > res; for (int i = 0; i < num.size(); i++) { int target = -num[i]; int front = i + 1; int back = num.size() - 1; while (front < back) { int sum = num[front] + num[back]; // Finding answer which start from number num[i] if (sum < target) front++; else if (sum > target) back--; else { vector<int> triplet = {num[i], num[front], num[back]}; res.push_back(triplet); // Processing duplicates of Number 2 // Rolling the front pointer to the next different number forwards while (front < back && num[front] == triplet[1]) ++front; } } // Processing duplicates of Number 1 while (i + 1 < num.size() && num[i + 1] == num[i]) ++i; } return res; }
上面的代码中,只需要跳过
front所对应的数字就好,因为back对应的数字会自然地随front变化而变化。Reference
-
每周算法:罗马数字转阿拉伯数字
Description
Roman numerals are represented by seven different symbols: I, V, X, L, C, D and M.
Symbol Value I 1 V 5 X 10 L 50 C 100 D 500 M 1000
For example, two is written as
IIin Roman numeral, just two one's added together. Twelve is written as,XII, which is simplyX+II. The number twenty seven is written asXXVII, which isXX+V+II.Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not
IIII. Instead, the number four is written asIV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written asIX. There are six instances where subtraction is used:Ican be placed beforeV(5) andX(10) to make 4 and 9.Xcan be placed beforeL(50) andC(100) to make 40 and 90.Ccan be placed beforeD(500) andM(1000) to make 400 and 900.
Given a roman numeral, convert it to an integer. Input is guaranteed to be within the range from 1 to 3999.Example 1:
Input: "III" Output: 3
Example 2:
Input: "IV" Output: 4
Example 3:
Input: "IX" Output: 9
Example 4:
Input: "LVIII" Output: 58 Explanation: C = 100, L = 50, XXX = 30 and III = 3.
Example 5:
Input: "MCMXCIV" Output: 1994 Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.
Solution
Approach 1
这道题不是很难,很容易就能想到解法,需要注意好边界条件问题,下面就是我的解法。
pint romanToInt(string str) { int ans = 0; int pos = 0; const int len = str.length(); // 千位 while (pos < len && str[pos] == 'M') { ++pos; } ans += 1000 * pos; if (pos == len) { return ans; } // 百位 switch (str[pos]) { case 'C': ans += 100; ++pos; if (str[pos] == 'D') { ans += 300; ++pos; } else if (str[pos] == 'M') { ans += 800; ++pos; } else { while (pos < len && str[pos] == 'C') { ans += 100; ++pos; } } break; case 'D': ans += 500; ++pos; while (pos < len && str[pos] == 'C') { ans += 100; ++pos; } break; default: break; } if (pos == len) { return ans; } // 十位 switch (str[pos]) { case 'X': ans += 10; ++pos; if (str[pos] == 'C') { ans += 80; ++pos; } else if (str[pos] == 'L'){ ans += 30; ++pos; } else { while (pos < len && str[pos] == 'X') { ans += 10; ++pos; } } break; case 'L': ans += 50; ++pos; while (pos < len && str[pos] == 'X') { ans += 10; ++pos; } break; default: break; } if (pos == len) { return ans; } // 个位 switch (str[pos]) { case 'I': ans += 1; ++pos; if (str[pos] == 'X') { ans += 8; ++pos; } else if (str[pos] == 'V') { ans += 3; ++pos; } else { while (pos < len && str[pos] == 'I') { ++ans; ++pos; } } break; case 'V': ans += 5; ++pos; while (pos < len && str[pos] == 'I') { ++ans; ++pos; } break; default: break; } return ans; }
不得不说,这样的代码比较丑,这是真的,就算解出来了成就感也不强。
Approach 2
这个解法是leetcode上最快的解法之一,只使用一个循环就完成了计算,代码整体上很简洁,也比较好理解。只需要针对6种特殊情况做特殊处理就好。
int romanToInt(string s) { int result = 0; int size = s.size(); for(int i = 0; i < size; ++i) { switch(s[i]) { case 'M': if(i - 1 >= 0 && s[i - 1] == 'C') result += 800; else result += 1000; break; case 'D': if(i - 1 >= 0 && s[i - 1] == 'C') result += 300; else result += 500; break; case 'C': if(i - 1 >= 0 && s[i - 1] == 'X') result += 80; else result += 100; break; case 'L': if(i - 1 >= 0 && s[i - 1] == 'X') result += 30; else result += 50; break; case 'X': if(i - 1 >= 0 && s[i - 1] == 'I') result += 8; else result += 10; break; case 'V': if(i - 1 >= 0 && s[i - 1] == 'I') result += 3; else result += 5; break; case 'I': result += 1; break; default:; } } return result; }
Approach 3
下面这个是我在看该问题的discuss板块的时候发现的。不得不说,结题思路实在新奇,这点是值得学习的。不过我比较担心它的时间复杂度。该方法使用Java编写。
public int romanToInt(String s) { int sum=0; if(s.indexOf("IV")!=-1){sum-=2;} if(s.indexOf("IX")!=-1){sum-=2;} if(s.indexOf("XL")!=-1){sum-=20;} if(s.indexOf("XC")!=-1){sum-=20;} if(s.indexOf("CD")!=-1){sum-=200;} if(s.indexOf("CM")!=-1){sum-=200;} char c[]=s.toCharArray(); int count=0; for(;count<=s.length()-1;count++){ if(c[count]=='M') sum+=1000; if(c[count]=='D') sum+=500; if(c[count]=='C') sum+=100; if(c[count]=='L') sum+=50; if(c[count]=='X') sum+=10; if(c[count]=='V') sum+=5; if(c[count]=='I') sum+=1; } return sum; }
-
每周算法:阿拉伯数字转换罗马数字
Description
Roman numerals are represented by seven different symbols:
I,V,X,L,C,DandM.Symbol Value I 1 V 5 X 10 L 50 C 100 D 500 M 1000
For example, two is written as
IIin Roman numeral, just two one's added together. Twelve is written as,XII, which is simplyX+II. The number twenty seven is written asXXVII, which isXX+V+II.Roman numerals are usually written largest to smallest from left to right. However, the numeral for four is not
IIII. Instead, the number four is written asIV. Because the one is before the five we subtract it making four. The same principle applies to the number nine, which is written asIX. There are six instances where subtraction is used:-
Ican be placed beforeV(5) andX(10) to make 4 and 9.
-
Xcan be placed beforeL(50) andC(100) to make 40 and 90.
-
Ccan be placed beforeD(500) andM(1000) to make 400 and 900.
Given an integer, convert it to a roman numeral. Input is guaranteed to be within the range from 1 to 3999.
Example 1:
Input: 3 Output: "III"
Example 2:
Input: 4 Output: "IV"
Example 3:
Input: 9 Output: "IX"
Example 4:
Input: 58 Output: "LVIII" Explanation: C = 100, L = 50, XXX = 30 and III = 3.
Example 5:
Input: 1994 Output: "MCMXCIV" Explanation: M = 1000, CM = 900, XC = 90 and IV = 4.
Solution
Approach 1
这道题并不难,方法也很容易想到,这道题被归为
medium难度反而让我感到有些奇怪,下面的代码就是我的解法。string intToRoman(int num) { // digit1 ~ 4 分别代表个十百千 int digit1 = num%10; int digit2 = num/10%10; int digit3 = num/100%10; int digit4 = num/1000%10; string ans; // 千 for (int i=0; i<digit4; ++i) { ans += 'M'; } // 百 switch (digit3) { case 1: case 2: case 3: for (int i=0; i<digit3; ++i) { ans += 'C'; } break; case 4: ans += "CD"; break; case 5: case 6: case 7: case 8: ans += 'D'; for (int i=5; i<digit3; ++i) { ans += 'C'; } break; case 9: ans += "CM"; break; default: break; } // 十 switch (digit2) { case 1: case 2: case 3: for (int i=0; i<digit2; ++i){ ans += 'X'; } break; case 4: ans += "XL"; break; case 5: case 6: case 7: case 8: ans += 'L'; for (int i=5; i<digit2; ++i) { ans += "X"; } break; case 9: ans += "XC"; break; default: break; } // 个 switch (digit1) { case 1: case 2: case 3: for (int i=0; i<digit1; ++i) { ans += 'I'; } break; case 4: ans += "IV"; break; case 5: case 6: case 7: case 8: ans += 'V'; for (int i=5; i<digit1; ++i) { ans += 'I'; } break; case 9: ans += "IX"; break; default: break; } return ans; }
这样做感觉有点简单粗暴,而且代码看起来不够优雅。
Approach 2
下面代码是从leetcode上找的,这样的打表法,看起来至少从形式上会更加美观,而且也非常好理解。
class Solution { public: const static string THOUS[]; const static string HUNDS[]; const static string TENS[]; const static string ONES[]; string intToRoman(int num) { string result; result += THOUS[(int)(num/1000)%10]; result += HUNDS[(int)(num/100)%10]; result += TENS[(int)(num/10)%10]; result += ONES[num%10]; return result; } }; const string Solution::THOUS[] = {"","M","MM","MMM"}; const string Solution::HUNDS[] = {"","C","CC","CCC","CD","D","DC","DCC","DCCC","CM"}; const string Solution::TENS[] = {"","X","XX","XXX","XL","L","LX","LXX","LXXX","XC"}; const string Solution::ONES[] = {"","I","II","III","IV","V","VI","VII","VIII","IX"};
Approach 3
下面这段代码也是leetcode上的答案,这个答案的通用性要好一些,最起码找到了规律,这有助于算法的后续拓展。
class Solution { public: string intToRoman(int num) { vector<int> base{1000, 100, 10, 1}; string roman = "MDCLXVI"; int index = 0, r; string ret = ""; while(num) { r = num/base[index]; num = num - r*base[index]; if(r == 4) { ret += roman[2*index]; ret += roman[2*index-1]; } else if(r == 9) { ret += roman[2*index]; ret += roman[2*index -2]; } else if(r >= 5) { ret += roman[2*index - 1]; // 下面这个string的用法值得学习 string tmp(r-5, roman[2*index]); ret += tmp; } else if(r < 5) { string tmp(r, roman[2*index]); ret += tmp; } index++; } return ret; } };
此外,我还学到了
string tmp(num, ch)这样的创建具有重复字符的字符串的方法。 -
-
静态成员变量初始化相关问题
引言
这篇文章的起因是出于对于
C++饿汉单例模式代码的一些疑问,查阅了一些资料。在仔细研究后,我发现在一些基础概念的理解还是存在偏差。
下面请看这样的一段代码,能看出其中有那些不太“正常”的语句么。class Singleton { public: static Singleton* getInstance(); private: Singleton() {} static Singleton* instance; }; Singleton* Singleton::instance = new Singleton(); Singleton* Singleton::getInstance() { return instance; }
私有静态成员的初始化
上面的代码是饿汉单例模式的
C++的实现,在没有查阅资料之前,我对其中私有静态成员变量的初始化存疑。主要有以下两点:- 为什么私有变量能够在类外被修改
- 为什么私有构造函数能够在类外被调用
在我之前的知识积累中, 私有的成员变量或成员函数是不能够在类外被访问的 。那么为什么以上代码没有问题呢?
在C++标准中找到了下面的一段话(可以在 C++11 standard 的 9.4.2节 或 C++ standard working draft 的 10.3.9.2节 中找到)
The initializer expression in the definition of a static data member is in the scope of its class.
这句话的意思是:静态成员变量的初始化是被看做为它自身的类域中的(
翻译的可能不是很准)。这样就不难理解为什么私有的静态成员变量能够在其类外被初始化了,由其私有构造函数进行构造也能说的通了。同样 ,在C++标准中给出了下面这样的示例代码:
class process { static process* run_chain; static process* running; }; process* process::running = get_main(); process* process::run_chain = running;
给出的说明如下:
The static data member
run_chainof class process is defined in global scope; the notationprocess::run_chainspecifies that the memberrun_chainis a member of classprocessand in the scope of classprocess. In the static data member definition, the initializer expression refers to the static data member running of classprocess.静态成员
run_chain定义在全局域;而process::run_chain则表示run_chain是process类的成员变量,从而处在process类的作用域中。私有构造函数
在查阅资料时,我发现 Peter 的 描述 纠正了我对私有构造函数的一些看法。
The point of a
privateconstructor is not preventing object construction. It is about controlling which code can access the constructor, and therefore limiting which code to create an object that is an instance of that class. Aprivateconstructor is accessible to all member functions (staticor otherwise) of the class, and to all declaredfriends of the class (which may be individual functions, or other classes) - so any of those can create an instance of the class using aprivateconstructor (assuming the constructor is defined).私有构造函数的目的并不是禁止对象构造,其目的在于控制哪些代码能够调用这个构造函数,进而限制类对象的创建。私有的构造函数可以被该类的所有成员函数(静态或非静态的)调用,该类的友元类或友元方法也能访问该类的私有函数,所以在上述情况中都可以通过私有的构造函数实例化出类对象。
- 为什么私有变量能够在类外被修改
-
客户端使用非阻塞socket进行connect的流程
问题
使用非阻塞(
non-blocking) socket尝试与服务端建立连接(connect)时,由于是io非阻塞的,所以connect函数会立即返回,那么如何判断client与server连接成功了呢?解答
客户端建立连接的示例代码如下:
int res = connect(fd, ...); if (res < 0 && errno != EINPROGRESS) { // case1. error, fail somehow, close socket return; } if (res == 0) { // case2. connection has succeeded immediately } else { // case3. connection attempt is in progress }
由于是非阻塞模式,所以
connect之后会直接返回,根据返回值res和errno能够判断建立连接的结果。- case1,表示连接失败;
- case2,表示连接建立成功;
- case3,表示正在建立连接的过程中,在这个情况下,需要等待socket变成可写(writable)状态,可以使用
select或epoll完成;
在 case3 情况下,socket可写后,执行下面的代码检查socket是否出现错误。
- case4和case5,表示socket出现了错误,将会关闭连接;
- case6,表示连接建立成功,可以开始
read和write了。
int result; socklen_t result_len = sizeof(result); if (getsockopt(fd, SOL_SOCKET, SO_ERROR, &result, &result_len) < 0) { // case4. error, fail somehow, close socket return; } if (result != 0) { // case5. connection failed; error code is in 'result' return; } // case6. socket is ready for read()/write()
参考资料
- case1,表示连接失败;
-
每周算法:最大容器
Description
Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
Example:
Input: [1,8,6,2,5,4,8,3,7]
Output: 49Solution
Approach 1 暴力解法
暴力解法是最容易想到的解法了,然而暴力解法肯定不是本题的意图。
int maxArea(vector<int>& height) { int ans = 0; int len = height.size(); for (int i=0; i < len-1; ++i) { for (int j=i+1; j < len; ++j) { int size = (j-i) * min(height[i], height[j]); ans = ans > size ? ans : size; } } return ans; }
使用这种解法只要把变量变化的范围想清楚就行了,没有什么特别的难点。
暴力解法的时间复杂度为 O(n2),空间复杂度为 O(1)。Approach 2
我在leetcode上看到这样一种解法,这种解法从逻辑和形式上看上不复杂,但是我的疑问在是否有严密的数学推导和论证。
int maxArea(vector<int>& height) { int ans = 0; int left = 0; int right = height.size()-1; while (left < right) { int w = right - left; int h = min(height[left], height[right]); ans = max(w*h, ans); if (height[left] < height[right]) { ++left; } else { --right; } } return ans; }
这个算法的主要思想是最大面积由两端边界较短的板决定;所以在移动边界时要将长板保留,移动短板。该算法的时间复杂度为 O(n),空间复杂度为O(1)。
在寻求该算法的数学推导时,我看到了 @nan15 给出的另外一种解释:
We starts with the widest container,
l = 0andr = n - 1. Let's say the left one is shorter:h[l] < h[r]. Then, this is already the largest container the left one can possibly form. There's no need to consider it again. Therefore, we just throw it away and start again withl = 1andr = n - 1.这个论证我认为是更加直观的:从最宽的容器开始,这时左边坐标
l = 0,右边坐标r = n - 1。假设左边更短,也就是h[l] < h[r]。那么,对于左边的板子,这是已经是它能够形成的最大的面积了,也就不需要再考虑它了。因此,将左边的板子丢掉,使用l = 1和r = n - 1重新开始。 -
为什么要使用各种前端框架
引言
在学习前端的过程中,我开始接触到许多开发框架或开发工具,这些工具让我开始眼花缭乱。使用常规的html/css/js就已经能够开发出这种网页了,所以我问自己,为什么要学习这些框架或工具,这些库是用来解决什么问题的。想明白这个问题,我学习的目的就更加明确,在遇到一些开发情景时,也能够快速准确地挑选出应该使用的框架。
下面按照我目前的理解,对目前的主流的前端开发库进行一些分析和比较。由于我还是一个初学着,所以我的观点可能还不是很成熟。
为什么要使用jQuery
jQuery是一个轻量级js库,它有如下特性:
- 简化了HTML/DOM操作
- CSS选择器
- 动画特效支持
- 解决跨浏览器的兼容行问题
- 完善的Ajax支持
在查阅资料的过程中,我还听到一些主张停用jQuery的声音。原因就在于随着前端开发生态不断的完善,现代浏览器原生API已经足够好用。
为什么要使用SASS
SASS是一种CSS预编译格式,它最终会编译成CSS。
SASS提供了CSS语法的拓展,它支持变量,算数运算符,循环操作,函数操作,样式模板(mixin)等强大的特性。它能够让开发人员更方便地编写CSS。SASS支持import关键字,这样就能够很方便地对样式进行模块化设计。加一句题外话,在使用SASS时,需要考虑的另一个问题就是代码物理结构的安排(直白的说就是目录的划分,源文件的存放位置等),这也是所有代码开发中需要注意的问题。
与SASS相似的工具还有LESS。
为什么要使用Bootstrap
Bootstrap是一个用于快速开发网页的前端框架。以我目前的理解来看,它更像是一个网页样式框架。
- 丰富的基础样式和资源
- 响应式(responsive),良好的移动端支持
- 强大的网格(grid)系统
- 一致性,保证跨浏览器的样式一致
为什么要使用React
DOM操作对性能的影响很大,频繁的DOM操作会使网页渲染的速度变慢,React主要解决了这个问题。
React.js允许在js中编写html,形成Virtual DOM,只在变化进行重新渲染。下面的一段文字摘自参考资料中的第5篇文章。
- Am I building an app which has lots of DOM interactions, or is it a relatively simple app with relatively few interactions?
- Does my app require a very high browser performance, that any user interactions must immediately be reflected in the UI? Is my data going to change over time, at a high rate?
- Is one user interaction going to affect many other areas/components in the UI?
- Is there a possibility that my app could grow big in the future, and so I would want to write extremely neat, modular front-end JavaScript that is easy to maintain? Would I want to use lots of native JavaScript or would I prefer using a lot of abstractions/methods provided in a framework?
- Would I prefer a framework/library which does not have a high learning curve and which is pretty easy to get started with development?
在使用React之前,问自己这样几个问题,就能够帮助你决定是否需要使用React。
- 所开发的网页应用涉及到很多DOM操作么?
- 开发的网页应用需要很高的性能么,这意味着任何用于的操作都要立刻反应在界面上?我的数据变更会很频繁么?
- 我开发的应用会在未来逐渐变得复杂么,这样我就需要将前端的js代码模块化?我是否会使用许多原生js特性,是否虚幻使用框架提供的抽象方法
- 是否需要一个学习曲线比较平缓的框架,能够方便地上手进行开发?
- 简化了HTML/DOM操作